Primary
Component and Extended Extra Focal Plane Source
Program GenerateBeamParameters
|
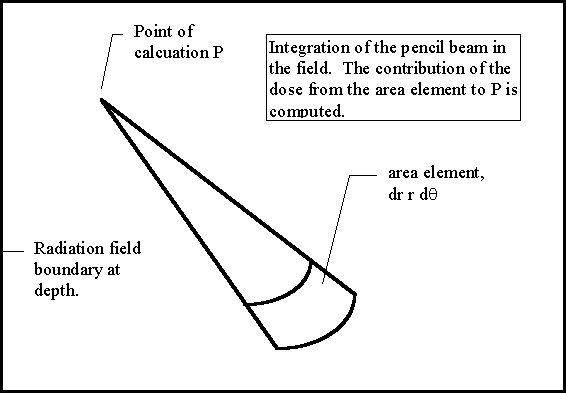
Figure 1 |
Dose Algorithm
The program uses a pencil beam algorithm. Below we will give details on how the pencil beam is developed from measured beam data and Monte Carlo calculated kernels. A single poly-energetic kernel is used to represent the pencil so that the algorithm can be fast. Calculating each energy separately with a spectrum and mono-energetic kernels would reduce the speed significantly. It is our philosophy that if greater accuracy is desired, one may as well use a Monte Carlo algorithm, so that there is a fast algorithm for quick results and a slow one for greater accuracy.
|
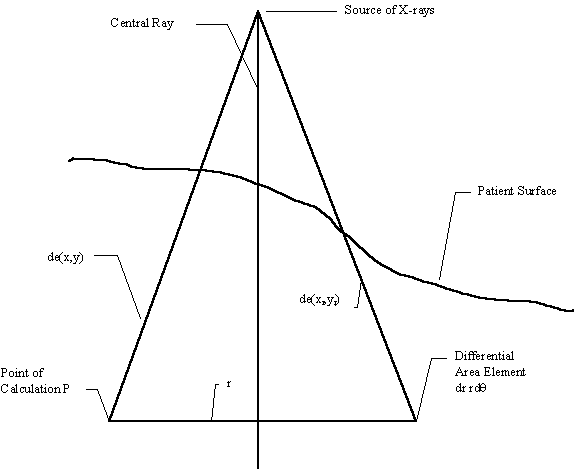
Figure 2 |
The dose is computed to the point P according to the below formula. r is the radius at depth from point P to the differential area element dr rdq. (x,y) is the coordinates of P at the treatment machine’s isocentric distance Sad. (xr,yr) is coordinates of the differential area element at distance Sad.
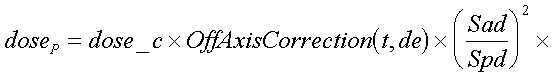
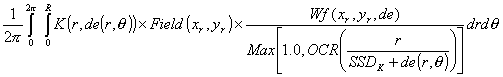
where
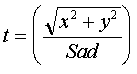
dose_c
In words, dose_c is the computed constant that converts everything that follows to give the calibrated dose for the calibration field size, SSD, and depth. The units of the pencil kernel therefore to not really matter. Dose_c is simply the ratio of the specified dose rate, usually 1.0 cG/mu, for some field size, SSD, and depth, to the result computed for the same field size, SSD, and depth.
Off Axis Correction
The Off Axis Correction is table developed from measured diagonal fan line data taken at depth for the largest field size. This two dimensional table is simply the ratio of measured over computed values stored as a function of the tangent of the angle with the central ray, t above, and depth. The depth de is the effective depth of the point of calculation P. de is computed by tracing along a ray from the point of entry into the patient body, and summing the incremental path length times the density at the location. This table provides a means of accounting for the change in beam penetration off axis since the kernel was developed from data on the central ray.
Inverse Square Law
The Sad/Spd squared term is the inverse square law, where Sad is the source axis distance of the treatment machine, typically 100cm. Spd is the distance from the source to the plane point P is in, along the central ray.
Kernel Integration
Next follows the integration of the pencil beam kernel over the area of the field. This formula is of course only symbolic. We can only integrate numerically on a computer, but the formula does show the mathematical idea. The kernel K(r,de(r,q))/2pr is the dose at the radius r at depth to the point P from the incremental area dr rdq. de(r,q) in cylindrical coordinates centered at P equals de(xr,yr) in Cartesian coordinates and is the equivalent depth along the diverging ray through the differential area element at the surface to the plane perpendicular to the central ray that contains the point P. We actually don’t have this kernel K, what we do have is the integration of K from 0 to r which is the dose at P from the circular disk of radius r at depth. So we actually take a difference here over dr in the numerical computation. Note that the r term cancels out and we have taken the 2p term outside of the integral.
Field
The differential area element is weighted by the field intensity Field at (r,q), here shown in the Cartesian coordinates (xr,yr) at the distance sad. For the Dosimetry Check program, this is looked up directly from the pixel value at that location from the measured field. In RtDosePlan this value is computed at each pixel location as the product of all devices that modify the primary fluence, with the end result the dose rate in cG/mu.
Primary Component and Extended Extra Focal Plane Source
The primary fluence is the sum of a primary source component plus the fluence from an extended extra focal plane source that may be down stream from the primary source. The primary source is multiplied by the transmission factor of any jaw, multi-leaf opening, or block that might be blocking the ray. The extended extra focal source is integrated over the area of the extended source that is visible from the point of calculation looking back through the collimator system, see reference 7. The collimator jaw opening, multi-leaf opening, and any blocks are considered in this integration. However, this integration is done for the point of calculation projected to the plane at 100 cm so that the integration is only done once for a single plane. Therefore small changes in the extra focal component with depth are not modeled. The addition of the extra focal source component to the primary component generates the scatter collimator factor. The exchange factor, between a 5x30 and 30x5 field for example, is modeled since the upper jaws project to this plane differently than the lower jaws. Also, the extended extra focal plane source is eclipsed differently than the primary source if down stream from the primary source. By modeling the effect here there is some improvement in the dose computed in the penumbra region and region just outside of the beam edge.
If the extra focal source model has not been fit (by routine FitExtraSourceModel), then the scatter collimator factor is simply looked up instead for the jaw opening, as will be shown below.
The extended extra source model is represented by an exponential intensity A x exp(-r x B) where A is a normalization constant and B is a parameter that is fitted. A primary source component Pr is also a fitted parameter. A is solved so that the in air scatter collimator factor will be 1.0 for the field size that the scatter collimator factor is normalized to (typically 10x10 cm). The distance of the extended source plane from the primary source is also a fitted parameter. The jaw transmission is also a fitted parameter when using the extended source model. Otherwise jaw transmission is assumed to be 1%.
The sum of the primary component and extra focal source component is then multiplied by the in air off center ratio. The total fluence F stored in the Field table is given by the equation:
F = (Pr x jt x mt + Iextf) x OCR
where Pr is the primary constant from above, jt is either 1 or the jaw transmission factor, mt is either 1 or the multi-leaf transmission factor. Iextf is the integration over the extended source function that is visible to the point of calculation after projection to the plane at 100 cm. OCR is the measured in air off axis ratio and is a function of the distance from the central ray.
If the extended extra focal source has not been fit, then F is simply given by:
F = In air collimator scatter factor x jt x mt x OCR
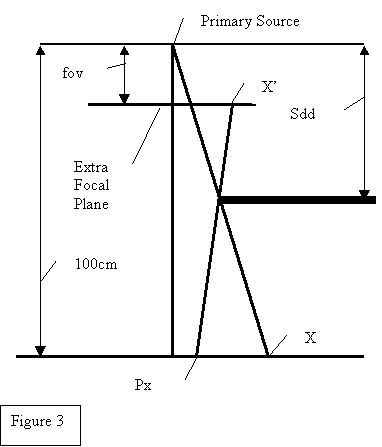
The integration of the extended extra focal source model is accomplished by projecting the beam defining contour to the plane of the extra focal source as seen from the point of calculation (but projected to 100 cm). The source to beam defining distance is needed for such contours and objects.
Consider the x coordinate of the point of calculation projected to the plane at 100 cm, Px. Consider a vertex of a beam defining object at distance Sdd from the source of x-rays. Project the vertex to the same plane at 100 cm, with resulting coordinate x. Let fov be the distance to the extended extra focal source plane. Then the vertex projects to the extended source model plane at X’, where
Sdd –fov fov X’ = (X-Px) -------------- +
X ------- 100 – Sdd 100
|
|
The multi-leaf contour and any block contours are truncated by the collimator jaw contour that is also projected to the extra focal plane (where the lower and upper jaws project differently because they are at different distances from the source). A bit map is created with a one set at a pixel for points on the extra focal plane that are visible to the point of calculation and a zero set if not visible. The exponential function is then simply added up over all the visible points. As this process must be repeated for every point in the Field array, the calculation time can become significant which is why this function is approximated for a single plane at 100 cm.
Wedge
Wf is the in air wedge off axis attenuation factor for the ray from the source to the point of calculation. However, this factor is reduced to affect a smaller wedge angle if an open field is being mixed with a wedged field to produce a smaller wedge angle. If there is no wedge than this factor is set to 1.0.
Given the wedge angle, the
wedge fraction fw is solved for (see reference number 8 below), where fw is the fraction of monitor units
due to the wedge:
Wedge monitor units = total monitor
units x fw
Open field monitor units = total
monitor units x (1.0 - fw)
fw = (1.0 - F) / ( 1.0 - F x (1.0 -
wf) )
where here
F =
1.0 - wedge angle / nominal
wedge angle
and
0 < = wedge angle <= nominal wedge angle
and wf is the transmission through the wedge on the central axis
in air (from the in air profile fitted by FitWedges).
The
transmission through the wedge at the off axis location, Wf, is given by:
Wf = 1.0 - fw + fw
x cw x wedge_transmission(xr,yr)
where cw is the wedge correction
factor as a function of field size and depth (from a table developed by
FitWedges). The wedge_transmission table
is developed by routine FitWedges to fit to in water data. The largest scan set across the wedge is
used to fit the transmission table in the point to heal direction. The other direction is corrected for the
increased slant depth through the wedge.
Wf is
therefore a function of position in the field (xr,yr) and
depth (due to the cw term) Slant depth is converted to depth parallel to the
central ray for looking up the cw term.
Kernel Correction for OCR.
The term in the denominator, the maximum of one or the in air off axis ratio (OCR) term, is to correct the kernel for having been derived from data that contains the effect of the OCR. Here we divide it out as long as the OCR has a value greater than one. The effect of most flattening filters on the OCR is that the in air fluence increases initially with radius. We want to correct for that effect. Otherwise for points on the central axis we could be effectively applying the effect of the OCR twice during integration over the area of the field, once built into the kernel and then formally through the above Field term.
But in the corner of the largest field the OCR value often decreases due to a cut off of the field due to the primary collimator. We do not want to cancel out that effect in those areas. The correction here is a compromise to achieve some deconvolution of the OCR term out of the kernel term. As the OCR is stored in terms of the tangent angle a ray makes with the central ray, we divide the radius at depth by the SSD used to measure the fields from which the kernel was derived from plus the effective depth along the ray from the differential area element to the plane perpendicular to the central ray that contains the point of calculation P.
Beam Fan Grid
Note that there are two effective depths used in the above equation. One is along the ray to the point of calculation P, de(x,y). The other is inside the integration (sum) and is traced along the ray from the surface to the differential area element dr rdq = de(xr,yr). The ray tracing along each ray is only done once. A fan line grid covering the area of the beam is created. Each fan line is ray traced through the patient with the storing of the accumulated equivalent depth at intervals along each ray. The spacing between the fan lines is set at a level half way through the patient to the dose matrix spacing value that the user can reset from the default value. Below this plane the fan lines are diverging further apart and above the plane the fan lines are converging closer together. Node points are distributed along the fan lines at equally spaced intersecting planes perpendicular to the central ray, and it is at these node points that the equivalent depths are stored. During the above numerical integration over each plane, the nearest ray is used to look up the equivalent depth. The same node points that hold the equivalent depths also define the points to be calculated. All other points are interpolated within this diverging matrix.
Approximations
Let us note here the approximations that are made. The integration is in the plane perpendicular to the central ray that contains point P. Rigorously it can be argued that the integration should be in the plane perpendicular to the ray from the source to the point P. For a worst case, the largest field size of 40x40, the ray at the edge of the field on a major axis makes an angle of 78.7 degrees instead of 90 degrees, an 11.3 degree difference, which is not going to make a large difference. The Off Axis Correction above will tend to cancel out such approximations. To be consistent, the Off Axis Correction is computed using the same algorithm. Using the inverse law correction for the slant depth along the ray from the source to point P made no difference from using the vertical distance parallel to the central ray. Another approximation is made below in the generation of the pencil kernel. It is assumed that at a depth d and radius r, the dose will be the same for a cylinder of radius r and for a diverging cone of radius r at the same depth. This is the same approximation made in the concept of Tissue Air Ratio.
Dose Matrix Arrays
Rectangular arrays of equally spaced points are generated for planar images, and a three dimensional lattice of points is generated for 3d perspective room views. The dose at these points are computed for each beam by interpolating within the above diverging fan line array of points generated for each beam. This means that in general the dose is interpolated between the eight corners of the diverging box that a point is inside. We will interpolate with less than eight points provided that the sum of the weights from the points is greater than 0.5, as some node points might fall outside of the patient. Once computed, each beam saves its dose matrix to a disk file, unless the beam is changed in which case a new fan line dose matrix array is created.
Generation of the Kernel
Program GenerateBeamParameters computes the pencil kernel from measured data. It does this in a two step process. We started with Monte Carlo computed mono-energetic point spread functions. We used those to computed mono-energetic pencil beam kernels. Next we take the central axis data at different field sizes to fit a spectrum. We constrain the spectrum to be a smooth curve by using a Gaussian (or normal) distribution, with the spread parameter different before and after the peak value, giving for parameters to be fitted: the peak energy value E0, the magnitude of the peak value A, the spread before the peak sl and the spread after the peak su.
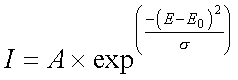
where
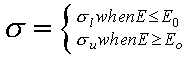
Using these kernels and spectrum to compute the dose, the dose at the surface is necessarily zero, whereas contamination electrons will result in some dose at the surface. At lower energy such as 6 MeV, the fitted spectrum with Monte Carlo computed kernels can reproduce the measured percent depth dose from dmax and deeper. However for higher energies such as 18 MeV, the contamination electrons have some effect still at dmax and deeper to 5 or 6 cm, causing differences of two to three percent at the small end or large end of the field size range. Without modeling the contamination electrons we cannot use this spectrum and mono-energetic kernels. We also have the consideration as stated above that computation time is saved by using a single weighted kernel. In doing so we give up the possibility of correcting for changes in spectrum off axis. Using off axis data one can fit a different spectrum at off axis intervals. The final consideration besides computation time is that the information measured with the Dosimetry Check program is dose on a plane perpendicular to the central ray, not the spectrum.
For these reason we instead generate a poly-energetic pencil kernel. The above fitted spectrum and mono-energetic pencil kernels are used for three purposes:
One, at 10 cm depth, which is beyond the range of contamination electrons, we can compute phantom scatter. This provides a means of separating the scatter collimator factor from the measured output factor for each measured field.
Two, we can compute the equivalency of circular fields to square fields, again at 10 cm depth, and use the resultant table to assign equivalent radii at each depth to the table of measured percent depth dose and square field sizes. We may now calculate an accumulated pencil kernel as a function of radius and depth from the measured square field percent depth dose data.
Three, we can complete the poly-energetic pencil kernel to zero field size, to a depth of 60 cm, and to a radius of 60 cm (the range for which the mono-energetic kernels cover), by scaling the results of the mono-energetic kernel and spectrum to agree where the tables join. From the surface to dmax the curvature computed at dmax is simply scaled to fit the end points from the smallest field and largest field in extending to zero radius and 60 cm radius respectively.
In this manner we produce a poly-energetic kernel which by design returns the same percent depth dose for all depths and field sizes measured.
Program GenerateBeamParameters
This program performs the above function of first fitting the spectrum and then using the result to assist in forming a poly-energetic kernel from measured beam data. After the poly-energetic kernel is created, this program computes the Off Axis Correction table from data measured in water along the diagonal of the largest field size at different depths. Next the program computes the dose using the specifications for field size, depth, and SSD, for the calibration definition and uses the result to compute the normalization constant that will convert computed results to cGray/mu. Lastly, the collimator scatter factor is computed by dividing computed phantom scatter into the output measured for each field size. The collimator scatter factor is used by program GenerateFieldDoseImage to compute the equivalent of a measured field which is to be used for testing purposes with program Dosimetry Check.
This program is an ASCII run program, meaning you run it in an xterm window with keyboard commands. The program will prompt you to select the treatment machine and then the energy. The program will take several minutes, most of the time spent in the initial step of fitting a spectrum. The program will stop if an error occurs, such as a needed file is missing. Be sure to check for error messages when the program has finished to ascertain that it was successful in computing all the output files that are required.
Program ComputePolyCAFiles
This is an ASCII program that will compare the dose in the central axis data files to that computed using the pencil beam. A report is produced that can be printed on a printer. This is an ASCII program that must be run from the keyboard in an xterm window. It provides a test that the kernel was properly generated.
Program FitWedges
This program fits the in air wedge profile curve given
measured in water scans. This program
is run after GenerateBeamParameters.
The wedge must be scanned for the largest field size across the wedge
(push the field size to the hardware limits) in water. An iteration procedure is used to fit the in
air profile to minimize the differences between computed and measured values in
the water data. The result is stored
in the file WedgeProfileAir_w0n_0e,
where n is the wedge number, e the nominal energy. A table is also generated for the other direction of the wedge to
correct for the slant through the wedge.
The change
in percent depth dose is corrected for with a wedge correction factor. For a range of field sizes, the measured
dose at depth is compared to that computed, and the ratio of measured over
computed is taken and stored as a function of field size and depth. This table is written to the file
WedgeCorrectionTable_w0n_0e.
Input data
consists of in water scan for the largest field size on the wedge, and central
axis measured dose for depths for different field sizes.
Program
FitExtraSourceModel
This program is run after GenerateBeamParameters. There must be available at least one scan of a square field. We suggest that there be a scan of a small field, such as a 5x5, a 10x10, and a large field such as a 30x30. The scans should extend several centimeters beyond the beam edge, 5 cm would be good. Given any distance to the extended extra focal source plane, this function fits the exponential source model so that the in air scatter collimator factor is reproduced. Note that the file Collimator should contain the correct source to collimator jaw distances. Then given the available profile scans for square fields, the extended source distance is found that gives the best fit to computed beam profiles. Both the distance and the jaw transmission is fitted in this step. The fitting process is then actually a nested iteration, fitting the source model for each possible source distance. The result is written to the file ExtraFocalSource0e, where e is the nominal energy.
References
1. T.R. Mackie, J.W. Scrimger, J.J. Battista, “A Convolution Method of Calculating Dose for 15-MV X-Rays”, Med. Phys., Vol. 12(2), Mar/Apr 1985, pp 188-196.
2. M.D. Altschuler, P. Bloch, E.L. Buhle, S. Ayyalasomayajula, “3D Dose Calcuations for Electron and Photon Beams”, Phys. Med. Biol., Vol. 37, No. 2, 1992, pp 391-411.
3. N. Papanlkolaou, T.R. Mackie, C. Wells, M. Gehring, P. Reckwerdt: “Investigation of Convolution Method for Polyenergetic Spectra”, Med. Phys., Vol. 20(5), Sept/Oct 1993, pp 1327-1336.
4. P.A. Jursinic, T.R. Mackie, “Characteristics of Secondary Electrons Produced by 6, 10, and 24 MV X-Ray Beams”, Phys., Med. Biol., Vol. 41, 1996, pp 1499-1509.
5. P. Bloch, M.D. Altschuler, B.E. Bjarngard, A. Kassaee, J.M. McDonough, “Determining Clinical Photon Beam Spectra from Measured Depth Dose with the Cimmino Algorithm”, Phys. Med. Biol, Vol. 45, 2000, pp 171-183.
6. T.R. Mackie, A.F. Bielajew, D.W.O. Rogers, J.J. Battista, “Generation of Photon Energy Deposition Kernels Using EGS Monte Carlo Code”, Phys. Med. Biol., Vol. 33(1), 1988, pp 1-20.
7. H. Liu, T. Mackie, E. McCullough, “Calculating Output Factors for Photon Beam Radiotherapy Using a Convolution/Superposition Method Based on a Dual Source Photon Beam Model”, Med. Phys., Vol. 24(12), Dec. 1997, pp 1975-1985.
8. R.D. Zwidker, et. al.,"Effective Wedge Angles for 6MV Wedges", Med. Phys., Vol. 12(3), May/June 1985, pp 347-349.
Acknowledgments
The author would like to here acknowledge the assistance provided by Dr. Thomas (Rock) Mackie of the University of Wisconsin, and Dr. Martin Altschuler and Dr. Peter Bloch of the University of Pennsylvania, with whom discussions were invaluable in learning how to compute with point and pencil kernels respectively.