Getting
Stereotactic Coordinates of Points
Delete
Stereotactic Frame Association
Stereotactic Frame
|
The Stereotactic Toolbar |
Select
the toolbar for the stereotactic frame under Options under Stacked Image Sets
on the main toolbar.
Stereotactic Frame File
You
must write a file for the stereotactic frame that you are going to use.† Example files are under the directory
frames.d in the program resource directory.†
The format of the file is documented in the example files.† See the ASCII file standard in the Program
Resources Files Chapter.† The comments
do not have to be present in the file but help to document what is in the
file.† An example stereotactic frame
file follows here:
/* file
format version: */ 1
/* name
of the system: */ <*example frame file*>
/*
Number of rods = */ 9
/*
Following below will be the diameter of each rod, and its end points.† The rods will be numbered by the below
order.
†††††††††††††††††††† All in Centimeters
Diameter† x††††††
y††††† z††††††† x†††††† y†††††† z */
0.9525† 14.0††††
0.0††† 9.25††† 14.0††††
0.0††† -7.65
0.635††† 7.36††
11.51†† 9.25††† 13.64†††
0.62†† -7.65
0.635††† 7.0†††
12.124† 9.25†††† 7.0†††
12.124† -7.65
0.635†† -7.0†††
12.124† 9.25††† -7.0†††
12.124† -7.65
0.635† -13.64†††
0.62†† 9.25††† -7.36††
11.51†† -7.65
0.635† -14.0††††
0.0††† 9.25†† -14.0††††
0.0††† -7.65
0.635†† -7.0††
-12.124† 9.25††† -7.0††
-12.124† -7.65
0.635††† 6.29†
-12.124† 9.25††† -6.29†
-12.124† -7.65
0.635††† 7.0††
-12.124† 9.25†††† 7.0††
-12.124† -7.65
/* Next
follows for the typical use of the frame the conversion matrix FROM the
coordinate system of the frame TO patient IEC coordinates.† This matix will typically be a rotation
matrix only.† The last row of:†† 0† 0† 0†
1††† is NOT entered.† This matrix is used for the purpose of
displaying patient IEC axes on a 3d view of the frame along with the frame's
coordinate system axes.† Locating the
rods on the images will establish the actual transformation between the
patient's coordinates and the frame's coordinates.
Here we
have a translation of (1.0, 1.0, 1.0) so that the two axes are not drawn on top
of each other initially.
*/
†††† -1.0††††
0.0†††† 0.0†††† 1.0
††††† 0.0††††
0.0†††† 1.0†††† 1.0
††††† 0.0††††
1.0†††† 0.0†††† 1.0
/*† color name for the system of rods: */†† <*seashell*>
/*† color name for a picked rod: */†††††††† <*red*>
/* The
following are material properties for the rods: */
/*
ambient */††† 0.5
/*
diffuse */††† 1.0
/*
specular */†† 0.0
/*
emission */†† 0.0
/*
shininess */† 0.0
/*
transparency (0 clear, 1 opaque */ 0.75
The
above is an example file and must not be used without confirmation and testing
as described below.
In
the file you must specify the coordinates of the end points of each rod and the
diameter of each rod.† To do so you must
determine each end of each rod in the coordinate system of the stereotactic
frame.† What the program does is solve
for a rigid transformation between the patient coordinate system and this
stereotactic frame coordinate system (see under Image Fusion for the definition
of a rigid transformation).† Points
located in the patient system can then be reported in stereotactic coordinates.
The file you
write completely determines what will be the stereotactic coordinate system
when you enter the rod coordinates.† You
must test the result.
In
the file you will also provide the first three lines of the transformation
matrix that will rotate and translate the stereotactic space to patient IEC
space.† This matrix should consist of a
3x3 rotation matrix with the last column representing a translation.† The last row is the vector (0,0,0,1)† which provides for translation in matrix
multiplication with vectors of the form (x,y,z,1) and is not written in the
file.† The IEC system has the positive Y
axis pointing toward the patientís head, the positive Z axis pointing anterior,
and the positive X axis pointing to the patientís left.† This transformation matrix must be provided
so that the program can draw in both the patient IEC axes and the stereotactic
frame axes on the same 3d view of the stereotactic rods.† This drawing will help you to turn the 3d
view of the stereotactic frame so that it is positioned similarly to its
presentation on the 2d images you will be locating the rods on.† The IEC axes will be drawn in the color used
for axes (defined in file FrameAxesColor in the program resource directory).† The stereotactic axes will be drawn in the unpicked
color of the rods defined, in the stereotactic frame file.
The
rods in the file will be numbered in the order in which they are listed in the
file.† A CT or MRI scan will represent a
plane that intersects the rods.† Where
the image plane intersects a rod, a cross sectional image of the rod will
appear in the image.† You will have to
locate on the image which rod is rod one in the file, and then which rod on the
image is rod 2 in the file, and so on for all the rods.† To do this you will pick each rod on a 3d
view of the rods, and then locate the corresponding rod on the image.† It may be important that you can orient the
3d view of the rods to correspond to the orientation as seen from the images.
Be aware of a
rod frame design that is symmetrical.†
If there is more than one orientation that matches the intersection with
images, you could mistakenly match the rods up with the wrong intersection
images.† To do so would result in an
incorrect solution.
Consider
for example the Leksell frame made by Elekta Instruments AB (Sweden).† The CT rod frame consists of side pieces
with two parallel lines and a connecting diagonal line.† There is also an anterior plate again with
two parallel lines connected with a diagonal line.† However, the anterior plane can move relative to the side pieces
and so moves relative to the coordinate system of the frame.† For our purposes this presents a problem
since we have to know the coordinates of the end points of the lines that show
up on the CT scans.† If the anterior plane
can move, than the coordinates can change and may be wrong.† Therefore you must either not use the
anterior plane or be sure that it is in a particular position for which you
have determined the coordinates (you might consider pinning or fixing the plate
to one position if you are going to seriously use this frame with this
software).† But without the anterior
piece, the side pieces are symmetrical; you can flip the system upside down
(head to feet) and the rods can still be matched up to align with the CT
scans.† But you would be matching the
wrong rod with the image of a rod.† You
would be determining stereotactic coordinates incorrectly, flipping points from
anterior to posterior and head to toe in this case.
The
program solves for the orientation of the rod frame mathematically without any
assumptions about the rod frame being parallel to or oriented in any particular
way with the imaging system.† This
removes the dependency of aligning the system in any particular way with the
imaging system and provides for a generic approach that will work with any
frame design.† Further, misalignments
during imaging are no longer a concern.
But
frame systems do generally attach to the patient in a particular
orientation.† The transformation matrix
between the stereotactic system and the patient IEC system provides a visual
clue for matching up the rods correctly.†
In our Leksell example above, the Leksell system has the positive Z axis
pointing towards the patients feet, the positive Y axis pointing anterior, and the
positive X axis pointing towards the patientís left.† The rotation and translation matrix from the Leksell stereotactic
coordinate system to the IEC system is thus:
|
1.0 |
0.0 |
0.0 |
-10.0 |
|
0.0 |
0.0 |
-1.0 |
+10.0 |
|
0.0 |
1.0 |
0.0 |
-10.0 |
|
0.0 |
0.0 |
0.0 |
†† 1.0 |
Note
that in the file the last line of the matrix is assumed and not entered, since
it will always be (0,0,0,1).†
Multiplying this matrix on the right by the column vector (x, y, z, 1.0)
will give the result (x -10, -z +10, y -10, 1.0), where we see that the x coordinate
remains the same, the new y coordinate is negative the z, and the new z
coordinate corresponds to the old y.†
Note that we moved the origin of the stereotactic system to the center
of the frame in IEC coordinates.† This
is just for convenience and appearance sake on the 3d view.
After
solving for the transformation between stereotactic coordinates and patient IEC
coordinates, the patient IEC coordinate axes are redrawn in the stereotactic
space on the 3d view of the rods in the position determined by the
solution.† This serves as another visual
clue to the correctness of the solution.
As
noted above, you are completely responsible for testing the program with your
frame file.† Particularly, if you are
going to locate points in stereotactic coordinates you must do a test with a
phantom to test the ability to locate points.
To
write a file for your frame, you could simply copy one of the example files and
use it as a template for making the new one.
Stereotactic Frame Test
Procedure
Choose
a phantom of some sort that you can put in the frame and on which you can
locate points that will show up on the scans.†
For CT you can use small lead markers.†
Place the markers on or inside the phantom.† But you will have to measure the coordinates of the these points
in stereotactic coordinates.† You can do
this either mechanically, or use a film method if the system provides a method
for determining coordinates from orthogonal films.† Also consider carefully how you determined the coordinates of the
rods.† A good test would be to use some
method provided by the stereotactic system for determining the coordinates of
the points to eliminate the possibility of performing the same error in
determining the end points of the rods and the coordinates of the test points.
Scan
the phantom.† You should use a small
slice spacing.† Make note of the fact
that the resolution perpendicular to the scans will depend upon the slice
spacing and is generally larger than the resolution in the plane of the
scans.† Locate the stereotactic frame
and solve for its position.† Then use
the points (under the stereotactic toolbar) popup to determine the stereotactic
coordinates of the points visible on the images.
Results
If
the scans are perpendicular to an axis in the stereotactic system, you may want
to compute the distance between the two determinations of each point both in
the plane of the scan and the three dimensional distance.† Let (stX,stY,stZ) be the coordinates of a
point determined from direct observation of the phantom or measured with the
stereotactic apparatus.† Let (pX, pY,
pZ) be the coordinates determined with this imaging system from the scans.† Let us assume that transverse scans were
taken and that they are parallel to the x,y plane of the stereotactic
system.† Then for each point compute the
in plane distance:
In
plane distance†† =†† sqrt( (stX-pX)*(stX-pX) + (stY-pY)*(stY-pY)
And
in three space for each point compute:
Three
space distance†† =†† sqrt( (stX-pX)*(stX-pX) + (stY-pY)*(stY-pY)
+ (stZ-pZ)*(stZ-pZ)
The
results should be of the order of the larger of the measurement accuracy for
determining the coordinates of the test points and the pixel size and slice
spacing.† The accuracy in plane is
limited by the pixel size of the images.†
The accuracy in three space is limited by the the larger of either the
pixel size or the spacing between the scans.†
In general, you should be within one millimeter for most of your test
points.
You are
responsible for establishing what the performance accuracy is for your
equipment using the above test procedure.
Select Frame
Before
locating a stereotactic frame you must first hit the New button on the
stereotactic frame toolbar to choose one.†
You will be presented a list of all the files that are in the program
resource directory frames.d.† Choose the
correct frame.† As there obviously can
only be one frame bolted to the patientís head (or one body frame in place),
there is only one frame possible per stacked image set.† You must select the one that was used.† Most likely, you have only one frame to
choose from.
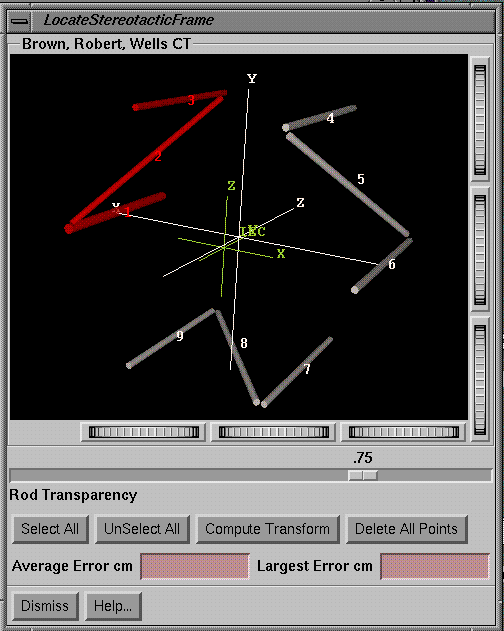
Locate Frame
|
Locate Stereotactic Frame Popup Tool |
Hit
the Locate button on the stereotactic frame toolbar to solve for the location
of the frame relative to the patient.†
The program solves for a transformation of coordinates between the
patient space, defined by the stacked image set,† and the stereotactic space.†
The transformation is rigid, with only rotation and translation allowed.
A
popup will appear that will include a 3d view of the rods.† The first time you should check this
carefully against the actual rod cage.†
Carefully inspect the 3d presentation against the actual object.† They should agree.† Note also the direction of the stereotactic coordinate axes
(shown in the same unpicked color) and the patient IEC axes (shown in the
default color for axes and labeled IEC).†
The axes should be oriented correctly relative to the rods.
You
can select specific rods by clicking the left mouse on the 3d view of the
rods.† The rod will change color.† You can unselect the rod by clicking again
on a selected rod.† You can select all
the rods or unselect all the rods with the SelectAll and UnSelectAll buttons.
For
the selected rods, click the left mouse on the corresponding image of each rod
in the 2d image from the stacked image set.†
Locate the rods in the same order that you selected them on the 3d view
of the rods.† If you had hit SelectAll,
the order is the numerical order of the rods.†
As you locate each rod on the image, that rodís color will change
back.† The select and unselect colors
are specified in the specific stereotactic frame file that you are responsible
for.
You
should locate all the rods in at least the first, middle, and last image in the
series of stacked images.† After
locating the rods on the images, hit Compute Transform to generate a
solution.† A rigid transformation
between the stereotactic frame and the coordinate system of the stacked image
set is solved for.† The images are not
solved for individually.† The relationship
among the images is known.† If there has
been patient movement during the imaging process some images may not align well
with the solution.† This will be evident
below when you project the frame onto all the images of the stacked image set.
From
the solution, the points that were located on the images will be transformed to
the space of the stereotactic frame and drawn in the 3d view.† Make the rods more transparent to increase
the visibility of these points.† The
points should all land within their respective rods.
Note
also that the average distance of the points from their respective rods is
computed, along with the maximum distance seen.† This should give you some indication of how well things are
going.† If you made an error and
associated a point with the wrong rod, you should see a larger average distance
and the maximum error seen should be large.
After
computing a transform you can add more rod location points and again compute
the solution again.
To
remove specific points from the list used for computing a solution, simply
click the left mouse on the point on the 2d display.† Note that the corresponding rod on the 3d display will not revert
back to a picked status.† You can delete
all location points with the Delete All Points button and start over again.
Verification of Solution
You
should then verify the correctness of your solution by examining where the rod
points you located on the 2d images fall within the 3d view of the frame on the
locate popup.† Then use Display Control
to view where the rods intersect all the images of the stacked image set.† In both cases the rods and their images
should correspond exactly.† If you have
made any kind of error, delete the solution and start over again.† The biggest source of error may be due to
associating the images of a rod with the wrong rod.† Or patient movement may have occurred during the image scanning.
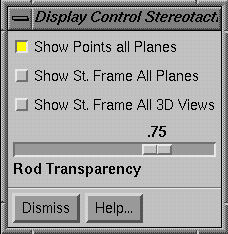
Display Control
|
Stereotactic Display Control |
Here
you can control what is shown about the frame with the stacked image set.†† The top toggle button controls whether or
not the location points are drawn.† If
you turn these points off, and then add more points, the new added points will
be drawn.† To turn them off first turn
all points back on and then all off again to catch the additional new points.
The
second toggle button will allow the frame to be drawn where it intersects an
image plane.† Use this feature to
further check the correctness of the found transformation between stereotactic
frame coordinates and all images of the image set.
The
last button will control the drawing of the frame in 3d views of the image
set.† The transparency scale is for
those views.† This does not effect the
3d view of the frame in the location popup.†
At this time we don't provide separate control over individual viewing
windows.†
Use
these tools described here and above to check the accuracy of the stereotactic
frame solution.
Getting Stereotactic Coordinates of Points
|
Get Stereotactic Coordinates for a Point Popup Tool |
Use
the Points button on the stereotactic tool bar to get the stereotactic
coordinates of a specific point that you locate with the mouse on an image that
is in the image set or is fused to the image set.† You have located the stereotactic frame in a stacked image
set.† Here when you locate any point in
that stacked image set with the mouse the stereotactic coordinates of that
point will be displayed.
The
stereotactic coordinates is the coordinate system of the stereotactic frame
defined by the corresponding file in directory frames.d in the program
resources directory.† The coordinate
system is defined by the coordinates of the end points of the respective rods
used for localization of the frame.
You
may also locate this point in any other stacked image set that is fused to the
stacked image set the frame was found in.†
Be careful that you understand which frame coordinates you are locating
a point in if that other fused stacked image set also has a frame.† You are finding the frame coordinates for a
point in the frame that belongs to the stacked image set that was current when
you selected the stereotactic frame option under "Options..."
Delete Stereotactic Frame Association
Lastly,
use Delete to remove the stereotactic frame from the image set.† You should remove the frame if any error
occurred concerning locating it.† You do
not want the association lingering around if it is not right.† When the program is restarted and the image
set is again selected, that association will remain unless deleted here.